Why We Can't Build Lasers on Silicon
Silicon's Achilles Heel is that its indirect bandgap prevents the implementation of high performance integrated lasers which are much desired in photonic integrated circuits.
Silicon technology has dominated for decades for its low cost and ability to scale, but it has its Achilles heel: you can’t build lasers on silicon.
Recently, we have seen a rising interest in silicon photonics; a field dedicated to manipulating light with silicon technology. Wider bandwidths in the optical frequency range allow for much faster communication networks which are immensely important in AI datacenters. Lidar technology would dramatically drop in cost if it could all be implemented in silicon. In the future, we might even replace electronic neural network training circuits with photonic processors that consume much lower energy.
All these ideas are encumbered with a lack laser source on silicon. Silicon is excellent for a whole array of photonic components; waveguides in silicon, optical modulators, filters and multiplexers can control light flow in the form factor of an integrated circuit. But the actual source of light itself needs to be built on materials better suited for laser generation using elements from groups III and V on the periodic table, such as Gallium Arsenide, or Indium Phosphide. It is then attached to the rest of the photonic circuit on silicon to create the “franken-chip” we call a photonic IC.
A fully integrated laser on silicon would be so much more convenient really.
In this article, we will discuss why we cannot build high efficiency silicon lasers (yet):
Principles of laser action
Energy bands, bandgaps and momentum
Direct and indirect bandgaps
More reasons why silicon does not lase
How bad is silicon really and what do we do?
Read time: 11 mins
Principles of Laser Action
Laser stands for Light Amplification by Stimulated Emission of Radiation, and is a process where atoms produce high energy beams of light in response to electricity, or to the application of light itself. A laser is a “light-amplifier” in a sense, where it produces a lot of photons for just a few incident ones.
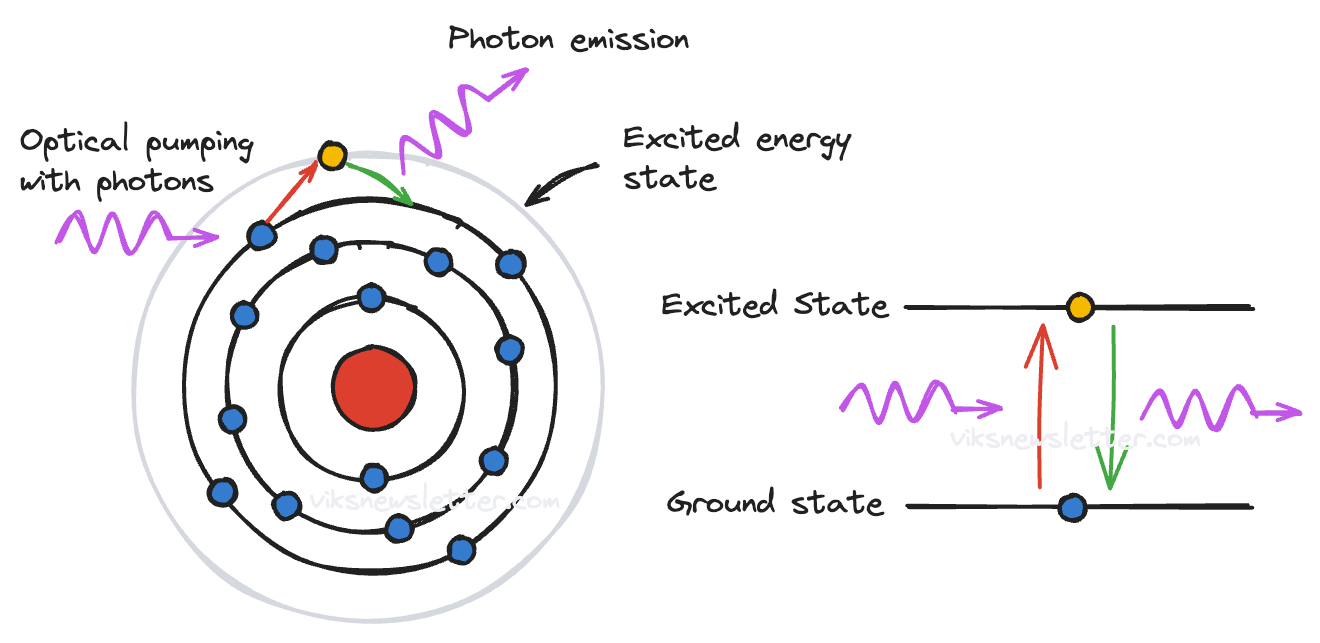
Laser generation is a quantum mechanical phenomenon, but the classical Bohr model of the atom is sufficient to broadly explain how the phenomenon works. The Bohr model is named after physicist Niels Bohr who proposed a simple model of the atom where the nucleus is at the center surrounded by orbiting electrons.
In this representation, electrons of certain materials capable of laser production are present in multiple orbits around the nucleus. The first step in the lasing process is to “pump” the electron in the outermost orbit. The pumping process can be done using light (optical pumping) or by passing current through the material.
When pumped, the outermost electron jumps to a higher energy orbit. If enough electrons in the material make the transition to higher energy states, they achieve population inversion. This excited electron stays in the higher energy state before dropping down to its original lower energy orbit and in the process releases a photon. The released photon travels through the previously pumped electrons triggering further discharge of photons but almost all at once. This cascade effect causes an avalanche of photons resulting in a focused beam of light called a laser.
The wavelength of laser light depends on the energy difference between the excited and stable electron energy states. The first laser demonstration was in 1960 by Theodore Maiman at the Hughes Research Laboratory which used a ruby rod optically pumped by a flash lamp. It produced short pulses of deep red visible light. The problem was that the flash lamp needed to be really bright for ruby to produce laser light. It required a lot of input photons to generate output photons. From a classical sense of an amplifier, it had low “photonic gain” and was therefore only of limited use. It still demonstrated the idea of how laser action works.
Today, ruby has been mostly replaced by better lasing media. Semiconductor lasers use III-V compounds such as Gallium Arsenide (GaAs) or Indium Phosphide (InP). Recently, variations of Gallium Nitride (GaN) such as Aluminum-GaN (AlGaN) or Aluminum-Indium-GaN (AlInGaN) have been used to generate laser light in the green, blue and ultraviolet regions, which are much higher in frequency than the original red laser generated by ruby. III-V compounds like these are well suited for laser action but not silicon. We will look at why in the rest of this article.
Energy bands, bandgaps and crystal momentum
With the understanding of how lasers work in single atoms, we can look at solids now.
Solids have many atoms held together by covalent bonds, which means that the outermost electrons are shared between multiple atoms. When two atoms are brought together in close proximity, their atomic nuclei exert forces on a shared electron. This results in energy splitting and the electron can now occupy two energy states above and below the original one. When a large number of atoms come together in a material, atomic interactions result in a band of closely spaced energies that electrons can occupy.
We can no longer talk about energy levels like in single atoms, but must instead think of energy bands in which electrons exist. Electrons exist in these discrete energy bands and the energies between them constitute the forbidden energy gap, where no electrons are allowed to reside. The difference in energy levels is called the bandgap energy, and is indicative of the amount of stimulus energy needed to move electrons from one energy band to another.

In any energy band that supports conduction, there is a sea of electrons that is available for charge conduction by moving through the material. But quantum mechanics states that a particle exhibits both particle and wave-like properties, in what is called the wave-particle duality. Thomas Young’s double slit experiment in 1801 showed that light can have diffraction and interference effects, proving the wave nature of light. In 1905, Einstein described photons as packets of energy observed earlier by Max Planck from blackbody radiation experiments, and was essential to explain the photoelectric effect. This phenomenon relied on light behaving as a particle.
If an electron can move through a crystal structure like a wave, then from wave-particle duality, it can be given a wave-vector k (that describes the propagation of the electron wave) and a corresponding wavelength called the De Broglie wavelength. Dividing Planck’s constant h by the De Broglie wavelength gives the electron’s crystal momentum. This is critical to why silicon does not lase, as we will see.
When you plot the energy of an electron versus its momentum for various discrete energy states, you get parabolic curves whose curvature depends on the electron’s effective mass1 in the solid material. The figure above shows several energy bands along a 1-dimensional axis in the crystal. In 3-dimensions, the energy bands resemble inverted or upright bowls in where electrons can reside.
Direct (in III-V) and Indirect (in Si) bandgaps
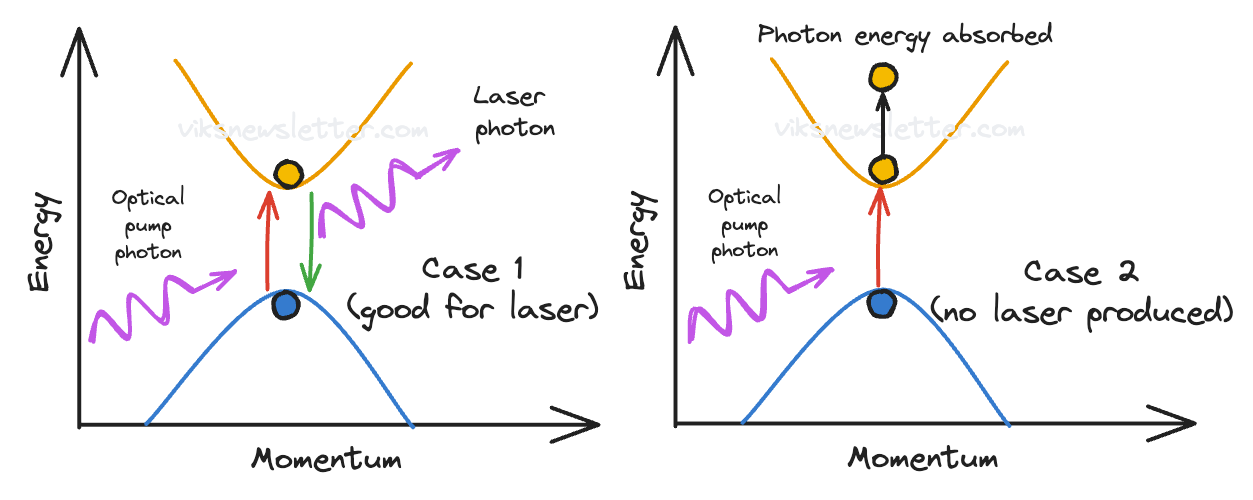
When the electrons in the lower band (with the inverted parabolic energy-momentum curves) are pumped with energy, they can transition to the higher band (with parabolic energy-momentum curves) by absorbing the energy only on one important condition: the momentum of the electron in both energy levels is the same.
The law of conservation of momentum applies to electrons. If momentum is not conserved, the pumped electrons must wait till something else can happen and make up for the difference in momentum. Most often, the mechanism that allows this to happen is a discretized vibration of the crystal lattice called a phonon. Phonons usually take much longer to arrive, in which time the excited electron loses its energy as heat and drops back to the lower energy level.

When the momentum of the two transitional energy bands line up, it is called a direct bandgap material because higher band is directly above the lower one, and the energy difference between the extremities of each parabola is the bandgap which the electron must overcome by absorbing a photon. This is fortunately the case in most III-V semiconductor materials which is why they make great laser media because of the ease with which energy transfer can occur between electrons and photons, while momentum stays conserved.
When the momentum of the higher and lower energy bands have different momenta at their parabolic extremities, it is called an indirect bandgap material. Silicon is an example of such a material, and lasing action is greatly reduced due to lack of momentum conservation. While phonons can provide the excess momentum required, the time taken for it to occur is too long for the electron to stay in the excited state.
Whether any given material has a direct or indirect bandgap depends on the arrangement of atoms in the crystal lattice, and is inherent to the material itself. And sadly, silicon does not have an optimal atomic structure for generation of laser light.
More reasons why silicon does not lase
Whenever a photon interacts with an energized electron, one of two things can happen:
The excited electron can drop to lower energy levels, and release another photon that causes more electrons to release photons resulting in lasing action.
The excited electron can absorb the photon and move to a higher energy level in the upper band.
These competing mechanisms depend on the material being used and determine the effectiveness of laser production. The former aids laser formation, while the latter does not.
In III-V materials, the curvature of the parabola is steep or you can think of it as a steep bowl in 3D that cannot hold a lot of electrons (observe the curvature of the higher energy band in the direct versus indirect bandgap diagram, in the last subsection). With the incidence of pumping photons, the electron bowl in III-V materials easily overflows. The electrons drop to lower energy levels and release light.
In silicon, the curvature is shallow and hence the bowl needs a lot more electrons to fill it up before lasing action begins. Here’s a more technical way to put it: silicon needs a lot more electrons in the excited energy state to achieve population inversion.
This fact has another consequence. An excited electron can lose energy to another excited electron present lower in the same energy band while giving up some energy as heat. This process is called Auger recombination and is more prevalent in silicon than in III-V materials, making it a worse laser material still.
How bad is silicon really and what do we do?
To be fair, it is not like silicon does not lase. It is just very inefficient at doing so. The mechanisms involved in energy exchange between photons and electrons are statistically low given the hurdles such as momentum conservation via phonons, higher population inversion levels and Auger recombinations that must be overcome.
Silicon needs a million electrons to be excited to produce one photon. In contrast, direct bandgap materials such as Gallium Arsenide need just two electrons to produce a photon. Clearly, silicon lasers are not feasible right out of the box, but that does not mean researchers roll over and give up.
The earliest demonstration of a silicon laser was in 2004 by a team of researchers in UCLA led by Bahram Jalali. Because silicon lasers need phonons to make up for the difference in momentum, they used light to induce atomic vibrations in silicon that can then be transferred to excited electrons to make up for the difference in momentum. By doing so, electrons in silicon are now able to transition to excited energy states and produce laser action. Subsequently, in 2005, Intel also demonstrated an all-silicon laser based on similar principles. See references for both UCLA and Intel papers on silicon lasers.
The interaction of light and vibrational modes of matter was discovered by Sir C. V. Raman for which he won the Nobel prize in Physics in 1930, and is called the Raman effect. As a result, such lasers are called Silicon Raman lasers. While it is possible to demonstrate laser action in silicon, their efficiency for most silicon photonics applications still remains low.
Today, integrated photonics technology uses heterogenous integration of III-V materials such as InP as lasers that are either bonded to a silicon photonics platform, or more recently, research has been focussed on growing these materials epitaxially in a silicon manufacturing process flow. For example, companies like Lumentum and Coherent specialize in providing laser sources for commercial silicon photonics platforms available from major foundries such as Intel, TSMC, GlobalFoundries and Tower Semiconductor.
References
[1] B. Jalali, “Making Silicon Lase,” Sci Am, vol. 296, no. 2, pp. 58–65, Feb. 2007, doi: 10.1038/scientificamerican0207-58.
[2] Silicon Lasers: The Final Frontier
[3] O. Boyraz and B. Jalali, “Demonstration of a silicon Raman laser,” Opt. Express, vol. 12, no. 21, p. 5269, 2004, doi: 10.1364/OPEX.12.005269.
[4] H. Rong et al., “An all-silicon Raman laser,” Nature, vol. 433, no. 7023, pp. 292–294, Jan. 2005, doi: 10.1038/nature03273.
If you like this post, please click ❤️ on Substack and subscribe to the publication.
Join our Discord community and get in on the discussion!
The views, thoughts, and opinions expressed in this newsletter are solely mine; they do not reflect the views or positions of my employer or any entities I am affiliated with. The content provided is for informational purposes only and does not constitute professional or investment advice.
The effective mass of a photon is related to its energy by the famous equation: E=mc^2.


Nice explanations! It has been a real problem.
Here is a review article on ways to try to put III-V materials together with Si. I think the monolithic trick at end, with trenches, is promising:
https://spectrum.ieee.org/lasers-on-silicon
Another trenching approach, also reported in 2023 is here:
https://www.nature.com/articles/s41377-023-01128-z.pdf
Looks like trenching will be a thing one way or another, more than one team seems close.
Damn, finally got some insight into phonons. It would be great if you can write an exclusive article just on Phonons. A term which I keep hearing from Optics people and Physicists, but being in Electronics undergrad, I was never exposed to this.